The Dangers of “Good” Science Communication

One of the central lessons I have learned from my time in the Skeptic community is that the veracity of information isn’t the primary factor in determining what people accept as true. Some groups have known this for a very long time. The practices of the advertising and marketing sectors are largely determined, whether they realize it or not, by the psychology of belief. In our highly connected, ad driven world, the importance of how to use the largely unconscious factors that affect attention and acceptance is central to success. This has worked its way into almost every aspect of our lives. One of my favorite science YouTube channels recently did a video about some of the things that affect the popularity of a video and interactions with the algorithm that determines how often that video is presented and to whom. The subject has also come up in print as various science communicators talk about the importance of headlines and the way they present information. As all of these people get better and better at presenting information in a way that appeals to our psychology they are able to make content that is more convincing and more likely to “go viral”. I see this as a significant, and essentially ignored, danger. People can be wrong. The more expertise you have in a field the less likely you are to be wrong. This is a particular danger in science communication. The material is often quite subtle. Without sufficient expertise in the subject material, it is likely that the message will misinform as much, or even more, than inform. This is fairly well understood and recognized, at least in the abstract. As Neil deGrasse Tyson put it recently in the ad for his MasterClass: “One of the great challenges in life is knowing enough to think you're right but not enough to know you're wrong”. As science communicators get better and better at presenting their material in a convincing manner the material is more likely to stick in people’s memories. When they present incorrect information, in this more convincing manner. their audience accepts it and remembers it even better. Let’s consider a specific, quite narrow, topic: waste from Thorium reactors. The amount of misinformation on this subject is enormous. I’ve seen trusted science communicators assert that the waste from thorium reactors is far less radioactive and has a shorter half-life than that of current reactors. This is not only wrong, it reinforces a fundamental misunderstanding of the subject. If something is less radioactive it has, by definition, a longer half-life. That’s simply what the words mean. It is impossible for something to be both less radioactive and have a shorter half-life. The half-life is the length of time needed for half of the sample to decompose due to radioactive decay. A substance with a very long half-life is very difficult to distinguish from one that is not radioactive. This mistake is often made in the opposite direction. You will see pronouncements about the danger of “highly radioactive materials with a long half-life”. Such materials, by definition, can not exist. One science communicator, popular among skeptics, explained that material in a thorium reactor is “completely burned” so it “has had almost all its radioactivity already spent”. As if radioactivity is a substance that is released in nuclear reactors. Not only is this not the way it works, it encourages people to think of reactors in ways that are simply wrong. Such misinformation can only make things worse. When that misinformation is skillfully communicated it does so to a greater extent. I have written about this type of problem before. That post was about the use of “whiz-bang” visuals, one of the many ways a video is made more appealing. So what can be done? A simple, fairly effective solution is both obvious and not practical. Restrict science communication to people that are true experts in the field being communicated. Another, slightly more practical option, is to get science communicators to confirm what they say with subject matter experts. Yet another option is for topics, like the characteristics of spent fuel from thorium reactors, which need lots of background information to be comprehensible, to be out of bounds for science communicators

Nuclear Waste as Nuclear Fuel? Not really.

I keep running across the assertion that nuclear waste can be used as nuclear fuel. In several cases it is asserted that it is only regulations that prevent this use. One went so far as to say "[W]hat’s the difference between nuclear fuel and nuclear waste. The scientific answer is really nothing, there is no difference. The only difference is a technological one. Nuclear fuel is radioactive material we know how to burn as fuel and radioactive waste is nuclear material we don’t know how to burn as fuel but there is no other real, physical difference between fuel and waste. It’s a technological difference only."

The quote in the previous paragraph is simply false. As will be explained below, nuclear waste, no matter what reasonable definition you use, contains a significant amount of material that cannot be used in a nuclear reactor. For the rest of this I'll address the more reasonable versions of the assertion.

To honestly make the claim that nuclear waste can be used as nuclear fuel several additional, and extremely important, details need to be added. Here's an overview. Details follow.

It is helpful to think of two types of fuel, active fuel and potential fuel. Active fuel undergoes a reaction that releases large amounts of energy, allowing the reactor to generate power. Potential fuel undergoes a reaction (or reactions) that convert it to an active fuel. In our day to day world only active fuel is thought of as fuel. Most current nuclear reactors use U-235 as active fuel and in normal operation almost all of it is used up. At the same time a small amount of the U-238, acting as potential fuel, is converted to Pu-239 that then acts as active fuel. All of the uranium originally put into the reactor is fuel but the vast majority is potential fuel and only a small amount of that either starts as or can be converted to active fuel in current reactors. It is sometimes said that the only difference between nuclear fuel and nuclear waste is the type of reactor it is used in. If by "fuel" we mean active fuel, which is the only kind we are familiar with in normal life, this is simply wrong. It is possible to build reactors where virtually all of the potential fuel is converted to active fuel but those reactors are complex and expensive and they require a large amount of complex processing to get anywhere near this point. It should also be noted that these future reactors can NOT be operated using only what we now call waste (more detail below). New, active fuel is needed.

The first problem is that the term "nuclear waste" means entirely different things to different people. For this discussion we'll be considering "spent nuclear fuel". This is a small fraction of the radioactive material produced in a reactor and is the only really problematic material short of a nuclear accident.

For this discussion we can consider most nuclear fuel as just a mixture of two isotopes of uranium. The majority is U-238, about 95% of it. It is potential fuel so it cannot take part in the power generating nuclear reactions. The rest, about 5%, is U-235. This is the active fuel that produces the desired energy in the reactor.

When the spent nuclear fuel is removed most of the U-235 has been used up, it is now <1% of the material. It is converted to what are called fission byproducts. This consists of a wide range of material, some quite radiologically hazardous, but for considerations of use as fuel it is worthless. Some of it is worse than useless. It will absorb neutrons, suppressing the desired nuclear reactions. It is truly waste. A small amount of the U-238 has been converted to plutonium, mostly Pu-239 with a smaller amount of Pu-240 and other isotopes. In total about 1% is plutonium. Some of the uranium is also converted to other uranium isotopes.

The claim that spent fuel is reusable is based on reprocessing. The idea is that by a variety of processes the spent fuel can be separated into components and then placed back into the reactors that it came from. Often the claim is made with numbers attached. Most commonly I've seen it as something like this paraphrased example: "Only around 5% of the energy available in nuclear fuel is extracted in our current reactors. 90% of rest could be extracted if the fuel were reprocessed". 

The 5% number should sound familiar, it is the original amount of U-235. The other 95% is based on the idea that the U-238 can also be used as a nuclear fuel. 

This is almost correct if we are careful when we talk about what kind of fuel we mean and, more importantly realize that it requires a type of reactor that is different than essentially all of the ones currently in use. The fact these issues are almost never mentioned when the claim is made is what makes the claim so misleading. 

To understand this better a bit more background is required. All of the reactors in this discussion are fission reactors. Nuclear fission occurs when a neutron is absorbed by a nucleus and that nucleus splits, roughly in half, and often emits a number of neutrons. There are many isotopes that will undergo fission but the important subset for this discussion are those that emit enough neutrons when they fission that a chain reaction is possible. These are called fissile materials. There are only a few such isotopes and three of them are most important for nuclear power: U-233, U-235 and, Pu-239. Of these only U-235 exists in any noticeable amount in nature. But there isn't much, it is just 0.7% of natural uranium. The remaining 99.3%, is essentially all U-238.

Most power reactors use uranium that has been enriched in U-235 to about 5%. This is done by separating out almost pure U-238, increasing the proportion of U-235. The separated material is known as depleted uranium. Enrichment is done so that the neutrons released by the fission are likely enough to reach another U-235 nucleus and cause a sustained reaction. This results in the 95% U-238 mentioned above. As mentioned above, the operation of the reactor results in some Pu-239 being created, some of it used as active fuel but about 1% of the the spent fuel is plutonium. 

The transformation from the potential fuel, U-238, to Pu-239, is a multi-step process.

U-238 + neutron → U-239
U-239 decays to Np-239 (half-life of about 25 minutes)
Np-239 decays to Pu-239 (half-life of about 2.5 days)

Near the end of the useful life of the nuclear fuel a significant fraction of the energy comes from the fission of Pu-239. It is possible to design a reactor to optimize the production of Pu-239. These are called "breeder" reactors and they produce more active fuel than the active fuel they consume. Breeder reactors sound too good to be true. Producing more fuel than is consumed doesn't seem possible, but it is. That's one of the problems with this entire topic. So much of what happens is so far outside of the intuition developed in our day to day world that we are often lead to conclude things that aren't true.

As an interesting aside, the oft mentioned Thorium reactor is also a breeder. Here Th-232 is a potential fuel that goes through a similar (but slower) multi-step reaction to produce the active fuel U-233, the third fissile isotope.

Current reprocessing of spent fuel produces, among other things, MOX fuel. These are Mixed OXides of uranium and plutonium, current reactors can use this material as a minority of its fuel. Almost all of this is produced by combining plutonium from reprocessing with depleted uranium. Depleted uranium is used because the uranium obtained from reprocessing (RepU) contains various impurities that impede the nuclear reactions and other negative consequences that are beyond the scope here. This is in direct contradiction to the common assertion that this MOX fuel is composed mostly of the reprocessed material and results in more of the potential fuel being used.

In conclusion, there is a lot of misinformation about nuclear power and so called "nuclear waste" much of that misinformation greatly exaggerates the dangers and problem. But a significant amount is being spread by nuclear proponents. Whereas it is possible to process spent nuclear fuel and extract virtually all of the nuclear energy available in the uranium fuel (both active and potential) this is far more complex and expensive than is implied by proponents, it would require reactors that are significantly different than those in use today, and it would not use all of material as fuel. 

Vaccination Fraction and the Base Rate Fallacy

I keep seeing references to the fraction of people with COVID related conditions that have been vaccinated. A recent story implied that the fact that about half of the infections in Israel were in vaccinated people was evidence that the vaccines aren't working. There is a nice post that looks at the stories about Israel. Half sounds like a lot only is you don't take into account the base rate of vaccination. Since 85% of the people have been vaccinated the fact that a far smaller fraction of the infected were vaccinated shows that the vaccines do work. Not taking the base rate into account, or deceptively not including it in the information provided, is the Base Rate Fallacy.

What is the relationship between vaccine efficacy, vaccination rate, and the fraction of those effected that are vaccinated? It turns out that it isn't as simple as you might expect.

Say the fraction of people that are vaccinated is v, and the fraction of illnesses the vaccine prevent is e. Then fraction of infected people that are vaccinated is:

Let's look at some examples. If we set both e and v at 0.85, meaning that 85% of the population has been vaccinated and that the vaccine is 85% effective in preventing disease. In that case the fraction of the cases that are vaccinated is expected to be just under half. For the current situation in the US let's take e=98% and v=30%. This gives us 0.008, which is a pretty good match for the oft repeated "99% of those hospitalized for COVID in the US have not been vaccinated".

I see a slight danger here. If we consider e=0.98 and v=0.5 we get 0.019. The vaccinated fraction more than doubles. The reason it goes up as the vaccination rate goes up is obvious, once it is pointed out. Take the extreme case, where everyone is vaccinated, v=1. Then the fraction of effected people that were vaccinated is also 100% since that's the only kind of people there are. This is the extreme case of the Base Rate Fallacy. I both hope and fear that when the US gets to v=0.5 we hear people using this doubling in the vaccinated fraction as evidence that vaccines aren't working. I hope for this because it will mean that v has gotten to 0.5 and I fear it will reduce future vaccinations. If we ever get to v=0.95 the fraction will be greater than 1/4, which will doubtless be trumpeted as a failure.

How do we get this equation?

Let's define some factors. Let's say that if G (for group) unvaccinated people are exposed we get Gc infections. That defines the degree of contagion c. If G vaccinated people are exposed there will be Gc(1-e) infections where e is the efficacy of the vaccine so we have a modified contagion factor of c(1-e).

If we have a group of N people then the number of cases expected in the vaccinated group, Cv, is Nv (the number of vaccinated people) times the modified contagion factor c(1-e).

The number cases in the unvaccinated group, Cu is N(1-v) (the number of unvaccinated people) times the contagion factor c.

So the fraction of cases that are vaccinated is the number of cases in vaccinated people divided by the total number of cases Cv/(Cu+Cv) or

There is a common factor of Nc so that cancels. So the number of people and the contagion factor don't enter into the final result. So we get: 

We could also divide through by (1-e) and get the expression at the top.

The Analemma

Most of us have seen an analemma though many are not familiar with the term. If you've looked at a globe or world map you've probably seen a curve that looks like a figure-8 somewhere in the Pacific Ocean. Like this (source: Wikimedia Commons):

The analemma is the path in the sky the sun follows at the same local time every day over the course of a year. This is the subject of some beautiful images. This one is tilted because the image shows the location of the Sun in the morning, not noon as will be used in the rest of this post.

If you haven't thought about it, it is hard to connect that statement with that shape. In fact, even if you have thought about it, it isn't easy. So what's going on here?

There are LOTS of explanations of this on the web that range from simplistic to opaque. They treat the subject with varying degrees of completeness and comprehensibility. I looked a lot of them and didn't find a single one that explained the features in a way that's comprehensive, correct, and accessible. So I decided to write this one.

Some things are easy to see. The Earth has a tilted axis that remains fairly fixed in orientation as it goes around the Sun. Except for areas near the equator, that means the Sun is higher in the sky in local summer than in the winter. For a lot of this discussion we'll be talking about the subsolar point, the spot on the Earth where the sun is directly overhead. This point is at its most northward at the June solstice and most southward at the December solstice. Each of those latitudes is removed from the equator by the tilt of the axis. The full range of this is just twice the tilt of the axis.

That explains most of what's going on but you might think that the sun would just move up and down in a straight line. There are three reasons that this isn't the case. None are obvious without a fair amount of thought and only one is explained well, or even at all, in most treatments of the analemma.

First we need to talk about one of my favorite bits of pedantry. When asked what the length of a day is on Earth most people have no problem coming up with 24 hours. And that's right, or almost right. The problem is that there at least three kinds of days. For most planets, including Earth, the day is determined mostly by the rate at which it rotates. In fact, when you look up the length of the day for any planet other than Earth what you often find is the rotation period measured with respect to the distant stars. This is called the sidereal day and for Earth this is 23 hours 56 minutes 4.09 seconds (approximately). So why do we say that a day is 24 hours? Are we just rounding up? No, that's not what's happening. There is a kind of day that is 24 hours, or pretty darn close. But we aren't there yet.

When people think of the word "day" they think about the time the Sun is above the horizon. At first blush you might think that the length of time it takes for the sun to go all around the sky is one sidereal day. But it isn't. That's because as the Earth turns it also goes around the Sun. Since both of these rotations are in the same direction it takes a bit longer for the subsolar point to return to (near) the same spot than one sidereal day. To make this clear, look at this. (source: Wikimedia Commons):

Marked "1" we see our Blue Marble with a marker pointed to the Sun. Next, at "2", Earth has rotated exactly once so it is pointing in the same direction as before but it has moved a bit around the Sun so it isn't pointed at the Sun. At position "3" it has rotated a bit more and it now pointed at the Sun. This take about four minutes. The time from noon to noon is called a Solar Day. Over the course of an entire year the number of sidereal days is one more than the number of solar days. (This figure is not an accurate representation of the motion of the Earth. The effect and relative sizes are distorted for clarity). So for a planet with a perfectly circular orbit and no axial tilt the Sun would trace the same path in the sky and be at the same point at noon every day.

But the Earth doesn't go around the Sun at a constant rate. It moves faster when closer to the Sun so it takes more time than usual to point back toward the Sun. This effect adds about 10 seconds to the length of a Solar Day in January and shortens it by about the same in June. This means that on some days it takes longer for the Sun to return to the same point in the sky, on others it takes less time. This produces side to side motion as seen in the analemma.

To see this explicitly, let's consider the point where the prime meridian and the equator cross. This is shown by the red pole pointing straight at the camera in the image below. The axis is the thick green pole and there are rings for the equator and the prime meridian.

If we look at the "Earth" (in quotes because there is no axial tilt) from the Sun once every average solar day we see two effects. The "Earth" changes size because the distance changes and it appears to rotate slightly. The spot where the Sun is overhead (subsolar) is indicated by a white dot.

It is easy to see some of the effect of a tilted axis. Let's consider the simplest case: A perfectly circular orbit with an axial tilt of 23.4°. Here are four images showing the situation at the equinoxes and the solstices.

We see that the Sun is overhead in the southern hemisphere in the first image, then at the equator, the northern hemisphere, and the equator again. So, we have the location of the Sun in the sky at successive mean Solar days moving north to south because of the Earth's tilt and east to west because of the elliptical orbit. This is where most explanations of the analemma stop. But it turns out that there are other effects. Even if our orbit were perfectly circular, the Sun's location at solar noon would still move east to west. This shift is also due to the Earth's tilt.

Let's look at a simple, but very exaggerated, situation. A planet with no axial tilt, a perfectly circular orbit, and a sidereal day 1/8 of its year. To start, as we did before, let's look from the direction of the Sun at local noon at the point with the red pole. 

Now let's move ahead one sidereal day. The axis is pointing in the same direction it was in the first image but the angle has changed.

If we advance forward to one solar day from the starting point it looks exactly like the first image. This gives the expected behavior. As we go through the year after each solar day that Sun returns to the same point in the sky.

But things are different when there is an axial tilt. Here's a set of images that show the differences. The ones on the left are the same those above. The ones on the right show what happens with a tilt of 45°. Starting at the time of the southern summer solstice so the planet has the southern hemisphere tilted the maximum amount toward the sun.

     Zero tilt                                           45 Degree tilt

The first four images are just we expect. For the top two the subsolar point is on the meridian and at a latitude that equals the axial tilt. The next two show the result of having revolved 1/3 of the way around the sun just as the planet has completed one solar rotation. But the last images are a surprise. At first we might expect the subsolar point to be along the marked line of longitude in both but isn't. The key to understanding this is to look at the axis. The North Pole has moved to the right and the subsolar point is displaced to the right of the meridian. If we look at the animation below showing an entire year of this, we see that the pole appears to shift both left and right as well as north and south.

If we look from this planet, along the direction of the red pole in the animation above we would see the Sun trace out the pattern seen below:

This computation was done with a circular orbit, all of the motion is caused by the large, 45°, tilt. If we try using the values for Earth, a tilt of 23.4° and an eccentricity (a measure of the non-circularity of the orbit) of 0.0167 we get this:

This is not the shape of the analemma as seen from Earth. It's pretty close, but not quite right. So, what went wrong? There is one more factor that affects the shape. We have taken into account the tilt of the axis producing motions in both the vertical and horizontal directions and the eccentricity of the orbit producing its own side to side motion. What we are missing is the relationship between the date of perihelion and the date of the solstice. For Earth, the southern solstice happens about 2 weeks before perihelion. In the computation above they happened on the same date. If we make this adjustment we get a good match:

This can produce some very different shapes. If we leave the date difference at 2 weeks, and increase the eccentricity to 0.3 and the tilt to 45° we get:

We can notice both the strange shape and the effects of the large eccentricity making the Sun change size by quite a bit.

I'll end this with one more simulation. Here is what the analemma looks like on Mars:

Freezing, Magnetism, and Viral Spread

 One of the things that I find most remarkable about science is how often disparate phenomena are connected in deep ways. The first two items in the title of this post are examples of a phase change. When the attractive forces between molecules, or the alignment of magnets, exceed the randomizing effects of temperature the system falls into a large scale order to form a solid or a ferromagnet.

There is also a strong mathematical connection to the epidemiology of a pandemic. The ability of an illness to spread is, in the abstract at least, just like the ability of magnets to align together or water molecules to freeze into a block of ice.

The study of phase changes is mathematically complex. One of the first, and simplest, techniques used to study this topic is called the Ising Model. It was constructed by Wilhelm Lenz in an attempt to model the formation of magnetic domains and assigned to his student, Ernst Ising. The model imagines a set of magnets that interact only with their nearest neighbor. Ising solved the simplest case, a one dimensional line, in his 1924 Ph.D. thesis, where he showed that there was no phase transition. He incorrectly concluded that the model was not able to produce a phase transition in any number of dimensions. The more complex two dimensional model was shown to have a phase transition by Rudolf Peierls in 1936 and solved by Lars Osanger in 1944. (The link in the previous sentence should not be followed by the mathematically timid) This shows a phase transition.

In its simplest form neighboring elements are given a probability of being aligned. Think of it as tiny magnets that have a tendency to face the same way but the random vibrations due to not being at absolute zero make this less than certain. 

The correlation of the magnets works out to be given by a mathematical function that deserves far more familiarity than it has; Hyperbolic Tangent (tanh). It looks like this:

The smooth transition from one state to the other doesn't seem like a good representation of a phase transition. But it is. The scale of the x axis changes with the number of elements in the simulation. For a large number of particles it looks like this:

One of the most surprising things, at least to me, is that freezing, or ferromagnetism, only happens if there are a large number particles involved. If the number of particles is small instead of there being a sudden transformation from one state to another at a well defined temperature there is a temperature range where the characteristics smoothly change from one state to the other. This behavior is captured very well by the Ising model.

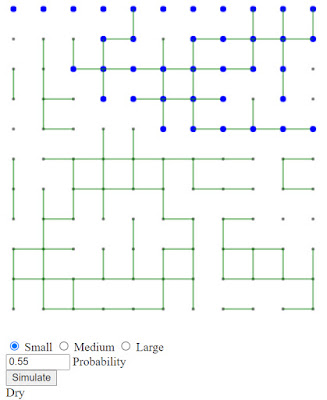
I've made an interactive webpage that shows a similar, but easier to compute system. Imagine a rectangular grid of points that can be connected by a pipe to the points on either side as well as above or below. Think of the top row as a source of water that can flow down, if the connections are there. The question is: Does the water make it to the bottom? Let's look at some examples to make it clear.

In this example there is a 10x10 grid with a 55% probability that any possible connection exists. In this case we see at the bottom of the image the word "Wet" indicating that (at least part of) the bottom row is "Wet". If we press "Simulate" sometimes the results are like the one above, other times like this:

If we run this many times with varying probability and note the fraction of the times the bottom is "Wet" at different probabilities. Here are some results for "small" grid with the probability setting ranging from 0.3-0.7:

The line is a tanh function adjusted to fit. It is very good fit to the points especially since I just eye-balled the adjustments for the tanh function and the data points still have some random noise since I only let the simulations run for a few thousand trials. As we vary the probability of a connection being present from 0.3 to 0.7 the fraction of "wet" final states changes smoothly from 0 to 1.

If we select "Medium" or "Large" the simulation uses 100 x 100 or 100 x 1000 points. As predicted by the Ising model the transition gets sharper and sharper.

Medium                                                               Large

       

This is instructive when thinking about epidemiology because it highlights a very unintuitive fact. When the percentage of people needed for disease spread to stop, often called "herd immunity" is considered this is not a gradual change. It is very much like the ability of water in the model above to get to the bottom. With a large enough group of people there is a sharp difference between a population that is protected from disease spread and one that is not. If herd immunity requires say, 65% of the population to vaccinated, it isn't true that 60% is pretty close. The population is either herd immune or it isn't.

Decoherence, Measurement, and a Collapse of Understanding

I frequently find myself getting quite upset when reading articles about Quantum Mechanics (QM) in the popular press and related media. This subject is very hard to write about in a way that allows the reader to grasp the elements involved without inviting misconceptions. In many cases I think that these treatments do more harm than good by misinforming more than informing. I know of no way to quantify the misinformation/information ratio but my experience as a science explainer tells me that the ratio is often significantly larger than one.

I recently came across an article that tried to tackle some very difficult topics and, in my opinion at least, failed in almost every case and spectacularly so in a few. There are so many problems with this article I had a lot of trouble deciding what to single out but I finally settled on this:

"However, due to another phenomenon called decoherence, the act of measuring the photon destroys the entanglement."

This conflation of measurement and decoherence is very common and the problems with it are subtle. This error masks so much of what is both known and unknown about the subject it is doing a disservice to the reader by hiding the real story and giving them a filter that will almost certainly distort the subject so that when more progress is made the already difficult material becomes even harder to comprehend.

So, what are "measurement" and "decoherence" in this context and what's wrong with the sentence I quoted? I'm going to try to explain this in a way that is simultaneously, accessible without lots of background, comprehensive enough to cover the various aspects, and, most importantly for me, simple without oversimplifying. 

"Measurement" seems innocuous enough. The word is used in everyday language in various ways that don't cause confusion and that is part of what causes the trouble here. When physicists say "measurement" in this context they have a specific concept, and related problem, in mind. The "Measurement Problem" is a basic unresolved issue that is at the core of the reasons that there are "interpretations" of quantum mechanics. There are lots of details that I'm not mentioning but the basic issue is that quantum mechanics says that once something is measured, if it is quickly measured again, the result will be the same. 

That sounds trivial. How could that be a problem? What else could happen? It is an issue because another fundamental idea in QM is that of superposition: A system can be state where there are a set of probabilities for what result a measurement will get and what actually happens is random. The details of the change from random to determined, caused by a measurement, is not part of the theory. In the interpretation that is both widely taught and widely derided, the Copenhagen Interpretation, the waveform is said to "collapse" as a result of the measurement. To say that this collapse is not well understood is a major understatement.

In summary, a quantum "measurement" can force the system to change its state in some important way. To use examples that you've probably heard: Before a measurement a particle can be both spin-up and spin-down, or at location A and location B, or the cat is both dead and alive. After the measurement the system will be in only one of those choices.

The word "decoherence" is less familiar. It is obviously related to "coherent" so it is natural to think of it as a process where something is changed so that it loses some meaning. A good example would be a run on sentence filled with adjectives and analogies that go at the concept from so many directions that meaning is lost rather than gained. That is not what decoherence is about. To explain what it is I need to provide some details of QM.

Quantum Mechanics can be described as a theory of waves. The mathematical object that encodes everything about a system is called a "wavefunction". Waves are another concept that is pretty familiar. Let's consider something that is familiar to many people: a sine wave.

There are lots of different sine waves, but they differ from each other in just three ways: Amplitude, Wavelength, and Phase. Amplitude is easy, it's just the "height" of the wave. These two waves differ only in amplitude:

Wavelength is easy as well. It is a measure of how "long" each wave is. These two waves differ only in wavelength. The red one is four times "longer" than the blue one:

Phase is less familiar. It is a "shift" in the wave. Here the blue one is "shifted" by 1/4 of a wavelength with respect to the red one. Note that it is the ratio of the wavelength to the shift that is important. Shifting a wave with a short wavelength by a fixed distance has a much bigger effect than one with a long wavelength.

From the perspective of QM these different characteristics are treated in very different ways. Without going into the reasons, here are some of the details. QM has a kind of mathematical automatic gain control. Amplitude is used to compute the probability that a measurement will have a certain value. This gain control ensures that all of those probabilities add to one. It is a bit of an overgeneralization but wavelength is the thing that defines the essential properties of the wave. Using light as an example, the wavelength of the light determines the color and (nearly) everything else about it. Phase is where (much) of the weirdness of QM comes from. Built deeply into the structure of QM there is no way to detect the phase of a wavefunction. Any two quantum mechanical "things" that differ only in phase cannot be distinguished by any measurement of the individual "things". But when they are allowed to interact with each other the effects can be dramatic.

If two waves of the same amplitude and wavelength but different phases are allowed to interact they add together to form a wave of the same wavelength but with an amplitude between zero and double the original amplitude. Here we see what happens if a red and blue wave of the same amplitude and nearly the same phase are added:

The resulting purple wave is about twice the amplitude of the starting wave. If the phases are arranged in a particular way the result is very different.:

The two waves cancel and the result is zero. These waves are said to be "out of phase" and they essentially vanish. As noted above, amplitude relates to the probability of measurement outcomes. If the amplitude is zero, nothing happens. It is as if the object isn't there. This is the essence of the double slit experiment. If you aren't familiar with this (or want a refresher on the subject), the link in the previous sentence gives a good introduction. Another term you will hear is that the waves "interfere" with each other and form an "interference" pattern. The different path lengths provided by the two ways light can reach a given spot on the screen smoothly change the relative phase so the result goes from being "out of phase" and dark to adding up to twice the brightness where there is constructive interference. When waves are combined and their phases have a slowly varying relationship the result is an interference pattern. A set of waves that have a fixed phase relationship are referred to as "coherent".

In this context the term "decoherence" is easier to understand. Decoherence occurs when the fixed relationship between the phases of elements of a system is lost. The phase of a wave is easily changed so this relationship is very delicate. Almost any interaction with the environment will affect it. This results in the destruction of any interference patterns in the results.

To recap, we are looking at two aspects of QM. First we have measurement. A quantum system can be constructed so that it is effectively in two states at once. This is often cited as a particle is spin-up and spin-down at the same time or Schrödinger's cat is both dead and alive. But once the measurement is made the results are stable. The system is seen to "collapse" into a known state. Next, we have decoherence where interactions with the environment cause changes in the phase of quantum waves and prevent interference patterns. 

So, let's look at that sentence again: "However, due to another phenomenon called decoherence, the act of measuring the photon destroys the entanglement.". Some of the possible states of a multi-particle system have a property called "entanglement". That is another topic that richly deserves its own rant but the details don't matter here. All we need to know in this context is that when one element in the system is measured it affects the entire system. In this case the "collapse", caused by the measurement, changes the system so that it is no longer entangled. The loss of entanglement is the result of the measurement. No matter how carefully interactions with the environment, the cause of decoherence, were eliminated the entanglement would still be lost.

If the situation is as simple as I describe, with decoherence relating to phase and measurement relating to collapse why are these concepts so often conflated? I think I understand the reason. 

The article quoted above is an exception but most of the time these concepts are confused it is in the context of why the quantum world and the day-to-day world seem so different. The weirdness of the quantum world is often divided into two categories. First, we have the ability of quantum objects to be in two (or more) states at once and the mysterious "collapse" to only one. Second, we have strange non-local behaviors. The double slit experiment has been done one particle at a time and the interference patterns persist. The particle, in some sense, is going through both slits at the same time. This effect, as described above, is exquisitely dependent on the system remaining coherent. It is easy to see why this effect goes away in the day-to-day world. The wavelength of an object gets smaller as it gets more massive. As noted above it is the ratio of the phase shift compared to the wave length that matters. This makes phase shift effects much larger and we get decoherence. The complexity of the day-to-day world is also important, there are so many particles that the number of possible interactions is enormous.

Less obvious is the first category, superposition and "collapse". There is a lot of work being done to try to explain why superposition and apparent "collapse" of QM aren't part of our normal day-to-day experience. It looks like decoherence is central to this situation as well. The details are subtle but it isn't, as implied by the quote at the start of this post, that decoherence causes the waveform collapse. It is that decoherence effectively removes all but one possible result from the available quantum outcomes. The term for this, explained here, is einselection, a portmanteau of "environment-induced superselection" This far from an easy read but it is, at least in my opinion, about as accessible as it can be. The unfortunate result is that decoherence, has become entwined (you might say entangled but the pun isn't worth it) with the concept of collapse and we get the conflation that this rant is about.

This treatment is far from complete but I hope it makes decoherence more comprehensible and shows how it is distinct from measurement and collapse, at least in the simplest cases.

The Fermilab Muon g-2 experiment

 Most of you have probably seen a story or post about the Fermilab Muon g-2 experiment. I have two problems with the way this has been treated by most science popularizers.

In keeping with the worst features of pedantry I'm not going to give a good explanation of the experiment in this post, just complain about certain elements in the coverage. For an explanation that avoids the first problem try this.

The first issue is pretty straightforward and, in the spirit of this blog, rather pedantic. In an attempt to explain what the experiment is measuring many stories describe gyroscopic precession as a "wobble". This is a mistake. Wobble is defined as an irregular (e.g.) action. The effect at the heart of the g-2 experiment is far from irregular. In fact it is extremely regular, so regular that it can be measured to an incredible level of precision. Without that level of precision the experiment would be useless to look at the phenomena involved. The use of a term that has irregularity at its heart in a story about extreme precision produces a level of cognitive confusion that cannot help but cause confusion. I suspect that most people don't realize that this confusion is an issue but I've seen this effect in many cases where the popular treatment of a subject produces lots of misunderstandings.

The second issue is more interesting. This experiment, if confirmed, reveals that our theories fail to accurately predict experiments. But the more interesting question is: What will fix this error? Every story, including the one I linked to above, says that this experiment may be pointing to the existence of unknown particles or forces that aren't included in the Standard Model. This is true but it ignores what I think is a far more exciting possibility.

If we look back at the history of physics, when there have been mismatches between theory and experiment, there are two different kinds of changes that were made to our theories. The first kind of change leaves the basic theory unchanged but changes some details like the contents of list of particles. In the Standard Model calculations that go into the theoretical predictions of g-2, every type of particle needs to be considered. The second kind of change to our theories is different. Rather then keeping the basic structure of the theory unchanged and changing the details, this possibility involves an entirely new theory.

An example, that is probably familiar to most readers of this blog, involves planetary motion. The details aren't important here but a detail of Mercury's orbit wasn't being predicted correctly by Newton's Law of Universal Gravitation. Previously, errors were noticed in the orbit of Uranus. Those could be eliminated if another planet was out there and this lead to discovery of Neptune. This was an example of the first class I'm talking about. In the case of Mercury the problem wasn't a missing input in our theory. The problem was that Newton's theory of gravity needed to be replaced by Einstein's. In the limit of small masses and low velocities Einstein's theory gives the same results as Newton's. But the theories are fundamentally different. They use an entirely different set of concepts to model reality. This new theory caused a fundamental shift in the scientific view of the cosmos and the birth of major new fields of science.

I don't have any reason to think that a new theory, one that reduces to the Standard Model in some limit like General Relativity reduces to Newtonian gravity, is going to be what is needed to explain the results of the Fermilab Muon g-2 experiments. But that is a possibility that shouldn't be ignored, instead I think it should be embraced. Who knows what wonderous changes it will produce in our view of reality?